- The axial force shall be determined on the basis of the condition P=T, where T is the amount of the reactive response of the ground when the screw pile is submerged, determined by the formula:
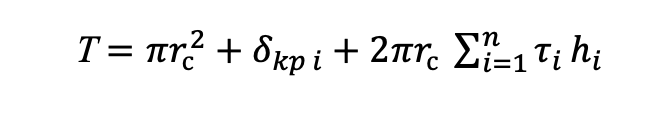
where

If the axial force P does not correspond to the reactive resistance of the ground when loading the screw pile T due to the difficulty of the Ground manual screw driver to maintain the equal axial force P and the reactive response of the ground, the failure of the axial force P, etc., then the further torque calculation shall be made according to the actual axial force P values.
This formula is the mathematics of ideal conditions, beautifully and logically reveals the principle of axial force operation and its direct dependence on the radius of the pile tube, the power of the ground and the pressure of the ground layers cut. In practice, however, it is not recommended for use in engineering calculations because it is a linear dependency formula that does not take into account a number of errors in practice.
- The torque value for loading the screw piles shall be calculated using the formula:
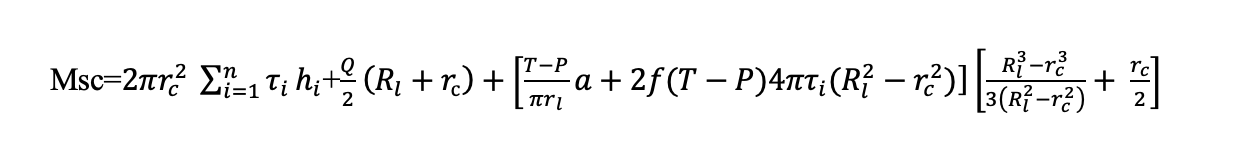
where

Q – reinforcement of the ground cutting by a screw blade determined by one of the formulas:
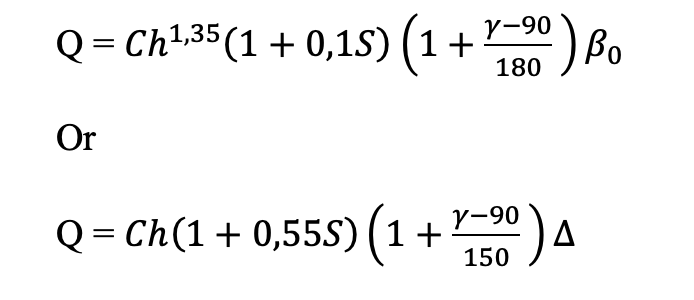
where

This formula is closer to a practical calculation, but…
- Based on mathematical statistics and correlation analysis methods, a formula with a higher accuracy of torque and axial force required for effective pile immersion is applied.
The torques required to dive the screw piles reach a maximum not only at the deep depth of the pile, but also, in many cases, when the pile blade passes through the densest and strongest ground. Therefore, the calculation is recommended to lead to the densest soils that can be met by a pile.
When the screw pile is immersed without the action of an axial force on it, it is immersed in the ground due to the overlying of the upper surface of the blade on the above ground. In one turn, the screw pile must be loaded to the size of the pitch of the blade. However, if the machine transmits only torque without axial force, then in one rotation the pile is loaded less than the pitch of the blade screw. When the pile is immersed by a machine capable of developing axial force, the pile at the beginning of the dive passes loose ground, where in one turn is moved by the amount of a large step of the blade screw. Then, as the pile deepens, the pile falls into more dense soils with greater resistance to penetration, and begins to put into the soils by the amount of first equal to the screw step, and then by a smaller screw step. To avoid this phenomenon, it is necessary to increase axial force with increasing depth of immersion.
If you create forces such that the resistance of the ground to the progressive motion at any moment of the screwing of the pile would be balanced by the axial force of the machine, then the force of friction of the blade against the ground and torque will be the smallest, and the speed of screwing of the pile the largest. Accordingly, the energy intensity of the screw pile dive will be minimal, and the efficiency of the screw pile lowering will be maximum. In this case, the pile in one turn will be submerged by the step of its helical blade. Consider the operation of the screw pile when it is in a homogeneous (perpendicular to the axis of rotation of the pile) ground with the same temperature and humidity at all points. The pile material is also homogeneous. Suppose that the tangent forces along the perimeter of the cross section of the pile and the normal voltages under the end of the pile are evenly distributed; the error of this assumption for the screw piles used in practice is likely to be negligible. The pile along the entire length, excluding the blade, has a constant size and the shape of the cross section. The screw pile blade is manufactured in accordance with the correctness of the geometric forms, without burrs, slag inclusions, etc. Taking into account these preconditions, we pre-determine the value of the axial force, and then the torque value for the required or calculated depth of the screw pile immersion into the ground. Considering that the axial force increment at the screw pile dive is a function of the variables defined by
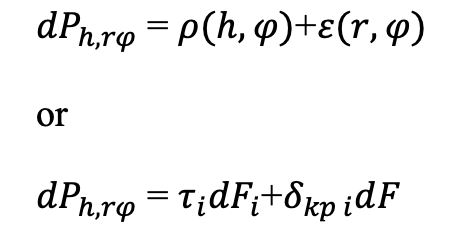
where

In its differential form, this equation has the following form:
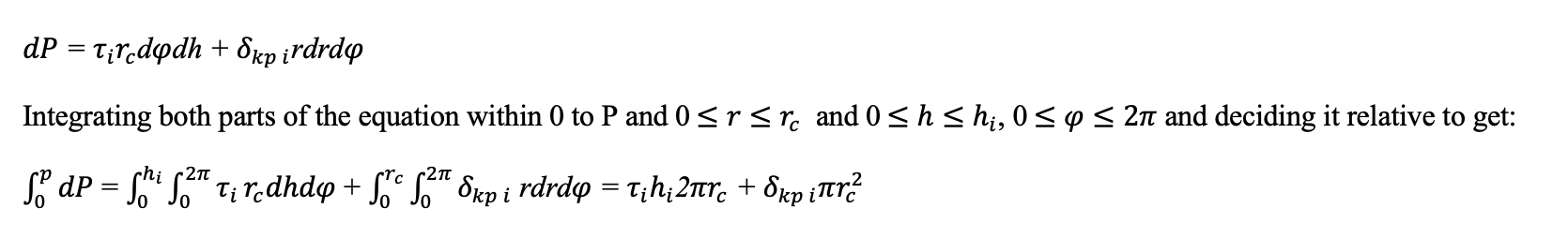
Finally, the axial dive force of the screw piles P can be determined by the formula:

The conclusion of the formula for determining the rational axial force required to dive the pile is based on the fact that the reactive force of the ground to dive the tube and the pile cone must be extinguished by the axial force of the machine sinking the screw pile, i.e. T = P (where T – ground reactive response, P – axial force). In fact T P (T = P only in the ideal case). This affects the torque of the pile dive. At P >T the torque is reduced and vice versa.
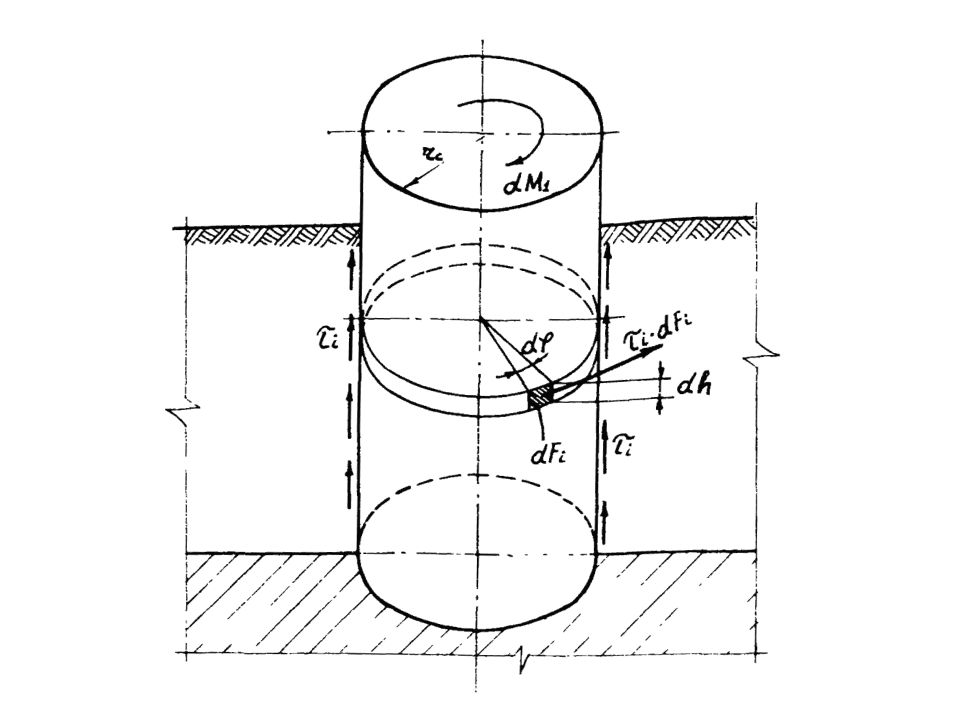
When the screw piles are loaded in the ground, the torque work is generally used to overcome the tangent forces of the soil resistance along the lateral surface of the tube and the blade of the screw pile, the forces of cutting the ground with a blade, rubbing the ground against the blade, active removal of the ground.
Calculation diagram for torque determination M
Thus,
where:

Elementary torque increment M2 are determined on the basis of a diagram of forces on an inclined plane:
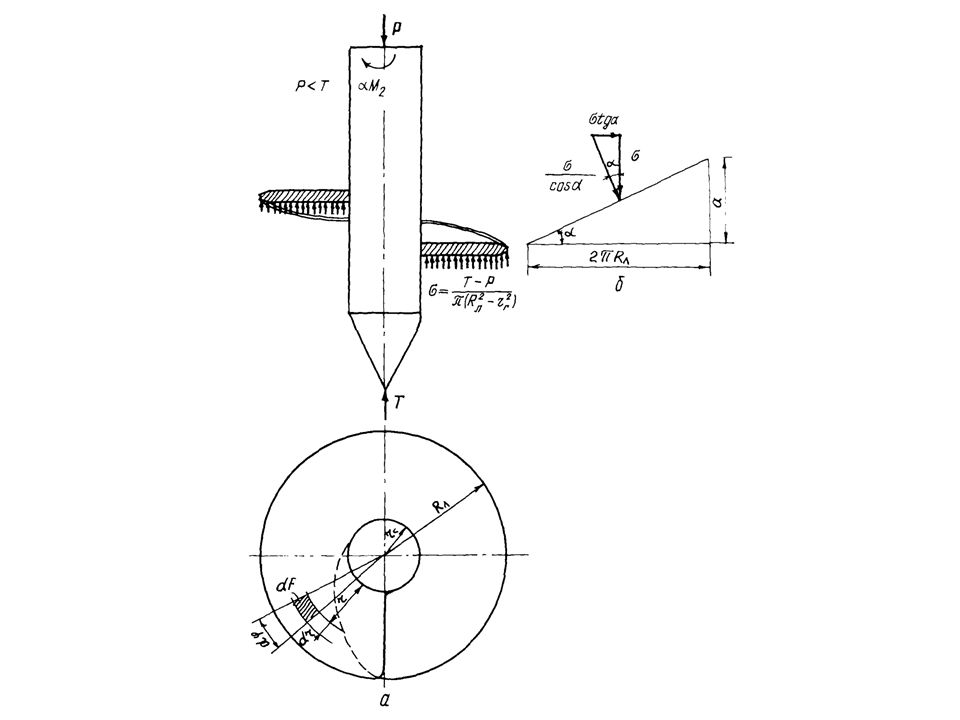

where a – pile blade screw pitch, m

Thus, the cutting force of the ground by the screw blade can be determined by one of the following formulas:


Attachment 1
Experimental values of the number of impacts C depending on the type, humidity, granulometric composition of undead soil
| soils | granulometric composition | humidity, % | С | ||
| 0,005 | 0,005-0,05 | 0,05-3,00 | |||
| Sandy loam | 7 | 60,3 | 32,7 | 14,1 | 1 |
| Sandy loam | 7 | 60,3 | 32,7 | 9,3 | 2 |
| Sandy loam (heavy) | 8,3 | 60,3 | 31,4 | 16,3 | 5 |
| Sandy loam (heavy, plant spreading) | 11,3 | 81,7 | 7,0 | 10,4 | 8 |
| Clay (some powder, pod) | 45,3 | 43,9 | 10,8 | 19 | 10
|
| Clay loam | 18 | 5 | |||
| Clay loam | 13,8 | 6 | |||
| Clay loam | 15,5 | 10 | |||
| Clay loam (easy) | 8,47 | 32,13 | 59,4 | 6,0 | 19 |
| Clay loam (middle) | 18,3 | 29,1 | 52,6 | 19,7 | 5,0 |
Experimental C impact values for frozen soils depending on their type, temperature, humidity
| soils | humidity | temperature, С | ||||||
| -1 | -3 | -5 | -10 | -15 | -25 | -40
|
||
| Sandy loam | 12
28 |
40-50
65-75 |
55-65
120-13 |
90-95
165-190 |
140-155
215-230 |
170-185
280-300 |
230-240
400-240 |
310-330
460-480 |
| Clay loam | 10
25 59 |
28-33
70-80 40-45 |
34-37
150-160 50-60 |
36-40
195-220 75-80 |
40-43
250-280 110-125 |
43-50
320-340 165-175 |
50-56
425-460 220-240 |
70-80
480-520 285-315 |
| Clay | 24
31 49 |
55-60
65-70 40-45 |
90-100
120-130 65-70 |
125-135
140-160 90-100 |
190-210
230-250 135-145 |
220-235
290-310 180-190 |
270-283
290-320 235-245 |
340-380
380-420 280-310 |
| Sandy | 8
11 18 |
25-30
50-55 150-160 |
35-38
65-70 200-210 |
40-45
85-90 220-230 |
50-53
95-100 240-250 |
55-60
100-115 260-280 |
60-65
120-130 285-300 |
70-75
140-150 325-340 |
Coefficient values depending on the blade angle
| Angle of cusp, | Coefficient |
| 180 | 1 |
| 120 | 0,96 |
| 90 | 0,90 |
| 60 | 0,83 |
| 50+15 | 0,81 |
(Extract from the Recommendations for Torque and Axial Force Determination of Screw Piles in Soils P462-82, All-Union Research Institute for Construction of Trunk Pipelines, 1983, Developers of Recommendations – candidate of technical sciences Spiridonov V. V., candidate of technical sciences Chernyuk V. P., engineers Pčelin V. N., Valčuk R. A.)
